Ever since I first visited Japan a decade ago, I have been fascinated by its approach to maths. The Japanese are, on the whole, more comfortable with numbers that we are in the West. Their elevated numeracy is a result of many idiosyncratic factors. Children, for example, are taught their times tables as a nursery rhyme, which seems to have the effect of lodging the numbers more deeply in the brain. Also, about a million Japanese attend after-school clubs to learn to use the abacus.

Another element of Japan’s numerate society is a unique culture of logic puzzles. Japanese logic puzzles — that is, pencil-and-paper puzzles with Japanese names based on grids that you need to fill in — are now known all over the world. Sudoku is the most famous, but open your daily newspaper and you will find others, like Kakuro and KenKen. Even though some of them are not originally from Japan (Sudoku was devised by an American, who called it Number Place), they were all refined by Japanese puzzle masters and became popular thanks to the Japanese market.

Researching my first puzzle book, Can You Solve My Problems?, I became fascinated by the work of Kobon Fujimura and Nob Yoshigahara, two authors from the 20th century who inspired the current generation of Japanese puzzle creators. I discovered the first four puzzles, right, in their books.

My interest in Japan led me to travel there this year to interview the most important people in the current puzzle scene. Over the past couple of decades, the Japanese have invented hundreds of wonderful grid-based logic puzzles, almost all of which are unknown outside Japan. My latest book, Puzzle Ninja, contains more than 200 of these puzzles as well as portraits of the creators.

The fifth puzzle, Walls, far right, is the invention of Naoki Inaba, the most prolific inventor of Japanese logic puzzles. I love this puzzle because of its minimalism and depth. All you are required to do is draw either a horizontal or a vertical line in each empty cell. Yet it quickly gets quite fiendish. I’ve included three examples, since it takes time to get used to the rules.

All the puzzles I’ve selected are based on grids. When it comes to Japanese puzzles, you don’t have to be square, but it helps!

Eight Neat Sheets

 
Eight sheets of identically sized square paper are placed on a table. Their edges form the following pattern, with only 1 sheet, marked 1, completely visible.

 
Can you number the other sheets from top to bottom where 2 is the second layer, 3 is the third layer, and so on?

The Square Digits

 
Using each digit from 1 to 9 exactly once, fill the grid so that each of the four equations are accurate.

A Square of Two Halves

 
A big square is divided into 16 smaller squares. The images below show two ways to cut this big square into two identical pieces

 
There are four more ways to do this. Can you find them? You must only cut along the inner lines, and the two pieces must be identical, not mirror images of each other.

Treading on the Tatami

 
Below is an arrangement of tatami mats. Find a path from A to B along the edges of mats that is even longer than the paths in the two examples. A path cannot go back on itself, or cross itself.

Walls

 
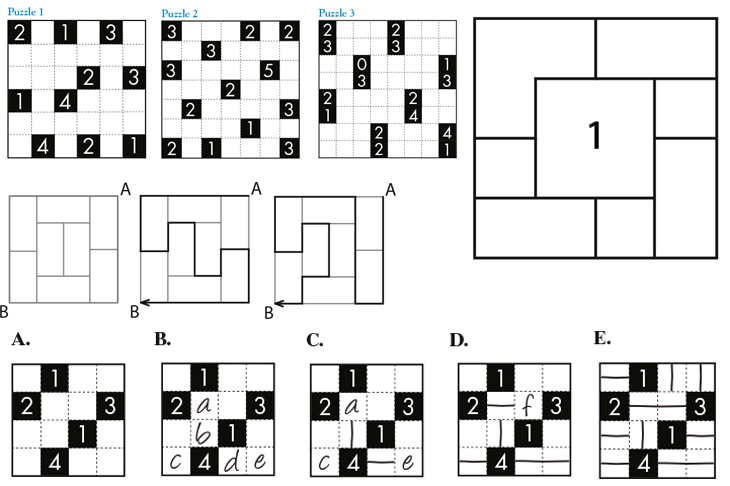
The challenge here is to fill each empty cell with either a vertical or a horizontal line so that the number in each black cell equals the combined length of lines ending at that cell. Lines cannot go through black cells. Here’s a tutorial on how to solve a simple one:

 
A. The starting grid.
 
B. The cells that can contain lines that may potentially end at the 4-cell are marked a, b, c, d and e. We can deduce that since the total length of lines ending at the 4-cell is 4, the lines must pass through b and d.
 
C. If the cell marked a has a vertical line, a line of length 2 ends at the 1-cell, which is forbidden, so a is a horizontal line, and thus c and e must have horizontal lines.
 
D. We can deduce that cell f must have a horizontal line since if it didn’t, there is no way for the total length of lines ending at the 3-cell to be 3. Once f has been filled in then the other cells fall into line.
 
E. The completed grid.
 
Here are three Walls puzzles handcrafted by Naoki Inaba from Puzzle Ninja.

 
To view the answers, please click here